Text generation and more specifically neural language modeling has recently exploded in popularity. The controversial release of GPT-2 coupled with the impressive generated text has brought language modeling to the forefront of NLP. A paper was recently released exploring the different sampling techniques for generating natural looking text, as well as proposing a new technique. The claims made by the paper were very interesting so I wanted to explore them a little bit more.
As a quick introduction language models are trained by maximizing the likelihood of a piece of text through the use of the chain rule of probability. $$ p(\mathbf{x}) = \prod_{i=1} p(x_i | x_0, ..., x_{i-1})$$
where $\mathbf{x}$ is a sequence of words or tokens from a dictionary of size $n$. We then parameterize $p(\cdot | \cdot)$ with some type of neural network (let's say $f$) and train it with maximum likelihood (which ends up being cross entropy loss for the conditional case).
For a second let's not worry about the training and imagine that we have a perfect language model. Well how do we generate realistic text from this perfect language model? We'll first try to formalize what it means to generate text from $f$.
Let's say that we want to generate some free form natural language seeded on some text. For example we can ask the model to generate text starting from the sentence "In the beginning the Universe was created. This has made a lot of people very angry and been widely regarded as a bad move." and we hope that it would generate something Douglas Adams-esque. Let's denote the context as $\mathbf{z}$. Keep in mind if we want to generate text completely from scratch we can have an empty context (usually only containing a beginning of sentence token).
So given that we have a function $f(z_{i+1} | z_{\le i})$ that can generate a probability distribution over the next token we should add to our context, which token should we chose?
Greedy Decoding/Beam Search
The most obvious thing to do would be to select the next token to be whichever token has the highest probability. $$z_{i+1} = arg,max_{z_{i+1}} f(z_{i+1} | z_{\le i})$$
Well what if we take a GPT-2 model and do greedy decoding starting from the example context we gave above.
> But now we are seeing that the Universe is not just created by the Universe, but also by the Universe itself. The Universe is not just created by the Universe, but also by the Universe itself. The Universe is not just created by the Universe, but also by the Universe itself. The Universe is not just created by the Universe, but also by the Universe itself
The model gets stuck on this one sentence and continues to repeat it. We might say that greedy decoding is not the correct way to maximize the likelihood because $$ argmax \ p(\mathbf{x}) = argmax \prod_{i=1} p(x_i | x_0, ..., x_{i-1}) \le \prod_{i=1} argmax \ p(x_i | x_0, ..., x_{i-1})$$
The maximum likelihood text is not the same as a text where every token is the maximum probability. Luckily this is a very well known optimization problem and the solution is beam search. We're not going to go deep into how beam search works but the quick gist is that it's a graph search algorithm that maximizes the probability of a sequence of tokens by doing a best-first search on the graph formed by selecting $m$ best tokens at each selected token recursively (where $m$ is the beam size).
Turns out running beam search on the same seed context produces almost the same exact text as greedy decoding. Let's discuss this phenomena a little bit more.
Importance of Surprise in Natural Language
Naturally very high probability natural language text will carry no information. Information appears when there are surprises in the text which would naturally have low probabilities of occuring (think self-information). In order for humans to communicate novel ideas, the sentences we speak cannot by definition have a high probability of occuring, otherwise it's not novel.
Grice’s Maxims of Communication (Grice, 1975) [has] established that people optimize against stating the obvious, making highly predictable text unlikely to occur in practice (The Curious Case of Neural Text Degeneration; https://arxiv.org/abs/1904.09751)
Following in the footsteps of Holtzman et al let's visualize the probabilities of a block of text from A Hitchhiker's Guide to the Galaxy and the block of text generated from GPT-2 seeded from the latter.
| GPT Probabilities on Real Data | GPT Probabilities on Generated Data |
|---|---|
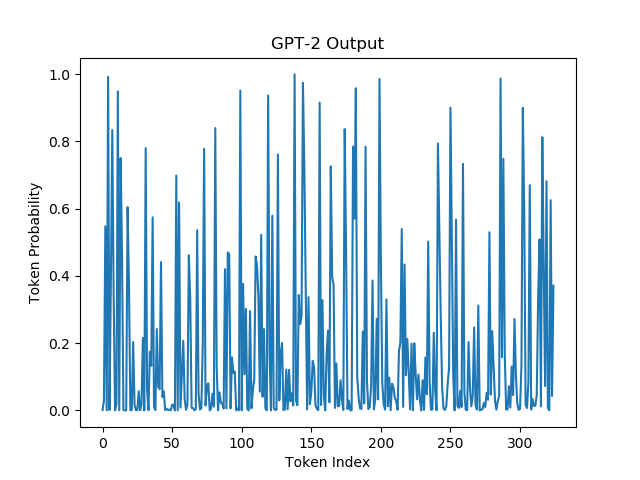 | 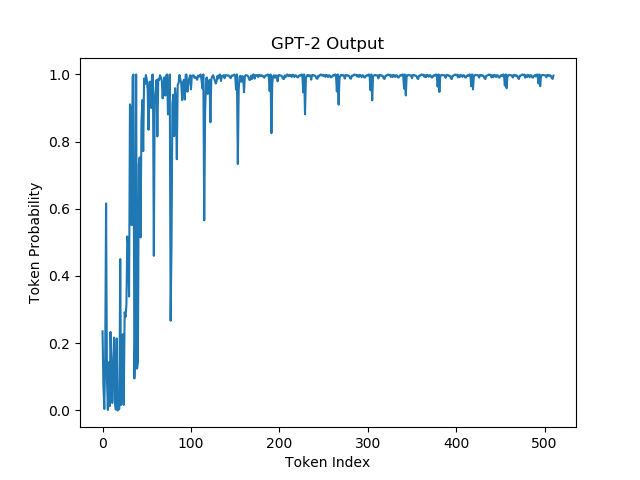 |
We're actually noticing two phenomena here:
- Beam Search/Greedy Decoding does too well and therefore produces samples that lack diversity and/or are repetitive.
- Unsurprisingly Beam Search started generating the same sentence over and over. Interestingly enough it seems like the model was stuck in a fixed point transformation, where the same sentence generated higher and higher probabilities every time it was produced. This was also noted by Holtzman et al and they called this repetition phenomena: The Gravitational Force of Repetition
- Repeated Sentence: "The next day, the girl was sitting on her own in a small cafe in Rickmansworth, and she was sitting on her own in a small cafe in Rickmansworth."
One a quick note, this might make beam search look like a flawed technique but this is not the case. Beam search works incredibly well in a constrained scenario (not when we're trying to generate free-form text) such as translation, where the output translated text is tightly coupled to the semantics of the input sentence. Even in other domains like semantic parsing where the logical form of the sentence is tightly coupled with the sentence itself beam search tends to shine. Beam search simply lacks the diversity that occurs naturally in language. But it's not a bug of beam search, it's a feature.
Introducing Diversity in Decoding
A trivial way to introduce diversity in our decoding algorithm is at every step to sample from the output distribution (without loss of generality let's not discuss the temperature parameter, which correlates to how much entropy is in the distribution). $$ z_{i+1} \sim f(z_{i+1} | z_{\le i})$$
Here's an example piece of text sampled with the same seed with a temperature of 0.9.
> It was even possible to allay the objections of a nameless racial minority who would not believe that doing what was right was impossible. There were also calls for a second prohibition on all the things anyone could buy on Earth selling for just $3.99. The folks who wanted to get their iPhones on shore after a robbery or an automobile accident.
The problem with this form of decoding is that accidently sampling a low probability token can cause non-trivial changes down the line, especially if the low probability token puts the model in a region that it hasn't seen before. This occurs quite often with language models trained via teacher forcing (methods to combat this effect have been researched; scheduled sampling, professor forcing).
Well if the issue is low probability tokens why don't we take the top $k$ tokens and sample from there? This simple adjustment to our sampling approach actually works surprisingly well. Let's use the same temperature and take the top 40 tokens at every step.
> But then this woman started to believe it was a stupid thing to be talking about: she began to think that, by telling her stories and making herself feel like a normal person, she'd be all-knowing and all-powerful, all-knowing that she'd saved the world and would soon be around to fix it.
This is much more coherent than sampling across all of the tokens. But can we do better? Holtzman et al argue that having a fixed top-k isn't a great idea because we don't take into account the model confidence. For example imagine if the model places a 0.9 probability on the next token being a certain token. We would still select $k$ top probability tokens and might accidently select a low probability token which would cause downstream issues. On the other side if the model is really unsure about the next token we would be limiting the models diversity by limiting it to only select $k$ tokens. So what can we do differently? Instead of fixing $k$ we can dynamically adjust it by asking that at every step $$k = arg\max_{k} \left[\sum_{i=1}^k sort_{descending}(f(z_{i+1} | z_{\le i}))_i\right] \leq k_p$$ the sum $k$ of the highest probabilities did not pass a fixed parameter $k_p \in \left[0,1\right]$. Holtzman et al call this nucleus sampling.
Below is an example piece of text:
> And then, on Friday, 11 August 2007, the world's leaders held a meeting to decide on a plan to remedy the problems of the planet. It was a technical conference in a big, oversized tree in the centre of London, with questions like "Should an automated telepresence system have existed?" and "Could an intelligent society exist without the use of digital watches?" and "If so, how?" and "Should we make electronic life devices available to people?" They came up with the idea to have a "society-wide standardisation" so that every two years there would be a population census of how many people people were living in all parts on a continent. But that's a long time to plan, and the calendar actually didn't make it.
After playing around with this type of sampling it surely is superior to the previous forms of sampling that we discussed. I'm glad to see a thorough analysis being done on the decoding methods. Beam search has been used blindly as a solution to all of our decoding needs for a while, I'm excited to see the new directions we can go in decoding.